3D 绘图投影类型

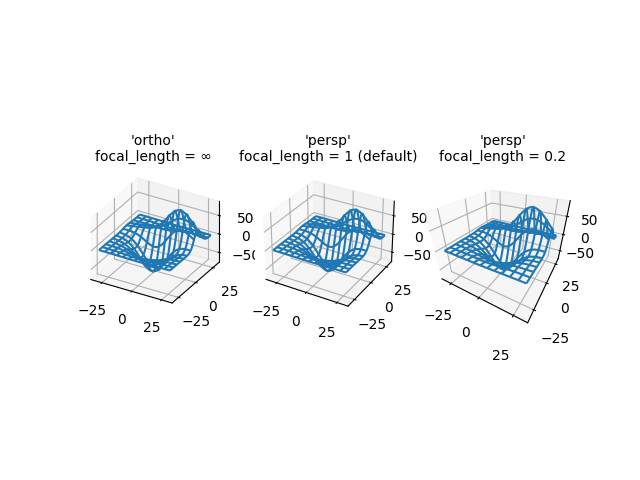
演示 3D 绘图的不同相机投影，以及更改透视投影焦距的效果。请注意，Matplotlib 纠正了改变焦距的“缩放”效果。

默认焦距 1 对应于 90 度的视场 (FOV)。在 1 和无穷远之间增加焦距会使图像“变平”，而在 1 和 0 之间减小焦距会夸大透视效果并赋予图像更明显的深度。在极限情况下，无穷远焦距对应于校正变焦效果后的正投影。

您可以通过以下公式从 FOV 计算焦距：

\[1 / \tan (\mathrm{FOV} / 2)\]

或相反亦然：

\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{focal length})\]

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt


fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})

# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot the data
for ax in axs:
    ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

# Set the orthographic projection.
axs[0].set_proj_type('ortho')  # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)

# Set the perspective projections
axs[1].set_proj_type('persp')  # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)

axs[2].set_proj_type('persp', focal_length=0.2)  # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)

plt.show()