笔记

单击此处 下载完整的示例代码

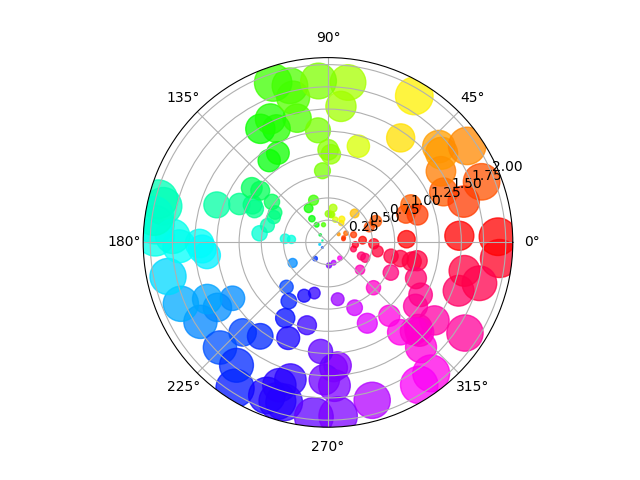
极轴上的散点图#

在此示例中，尺寸呈放射状增加，颜色随角度增加（只是为了验证符号是否正确分散）。

import numpy as np
import matplotlib.pyplot as plt


# Fixing random state for reproducibility
np.random.seed(19680801)

# Compute areas and colors
N = 150
r = 2 * np.random.rand(N)
theta = 2 * np.pi * np.random.rand(N)
area = 200 * r**2
colors = theta

fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
极地散射

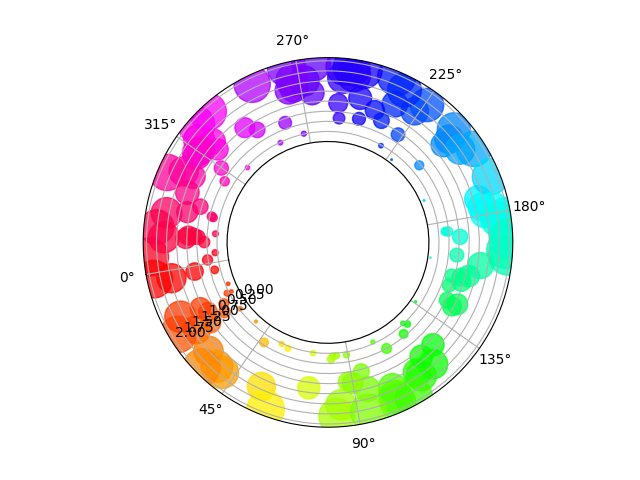
极轴上的散点图，具有偏移原点#

与上图的主要区别在于原点半径的配置，产生了一个环形。此外，θ 零位置设置为旋转绘图。

fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)

ax.set_rorigin(-2.5)
ax.set_theta_zero_location('W', offset=10)
极地散射

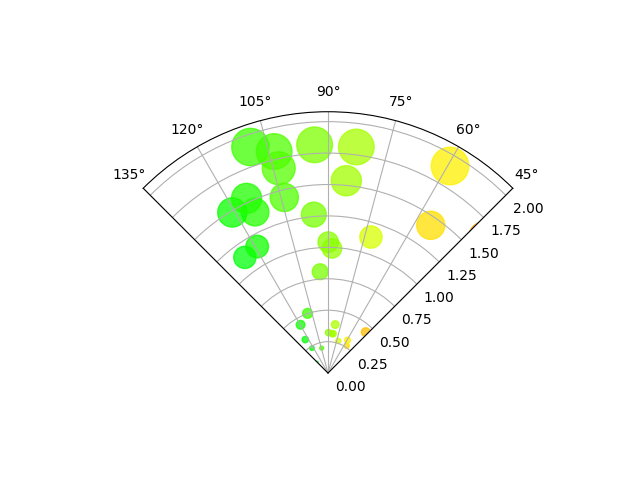
极轴上的散点图仅限于一个扇区#

与前面的图的主要区别是 theta 开始和结束限制的配置，产生一个扇区而不是一个完整的圆。

fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)

ax.set_thetamin(45)
ax.set_thetamax(135)

plt.show()
极地散射

参考

此示例中显示了以下函数、方法、类和模块的使用：

脚本总运行时间：（0分1.739秒）

由 Sphinx-Gallery 生成的画廊