笔记
单击此处 下载完整的示例代码
雷达图(又名蜘蛛图或星图)#
此示例创建一个雷达图,也称为蜘蛛图或星图[ 1 ]。
尽管此示例允许使用“圆形”或“多边形”的框架,但多边形框架没有正确的网格线(这些线是圆形而不是多边形)。可以通过将 matplotlib.axis 中的 GRIDLINE_INTERPOLATION_STEPS 设置为所需的顶点数来获得多边形网格,但多边形的方向与径向轴不对齐。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle, RegularPolygon
from matplotlib.path import Path
from matplotlib.projections.polar import PolarAxes
from matplotlib.projections import register_projection
from matplotlib.spines import Spine
from matplotlib.transforms import Affine2D
def radar_factory(num_vars, frame='circle'):
"""
Create a radar chart with `num_vars` axes.
This function creates a RadarAxes projection and registers it.
Parameters
----------
num_vars : int
Number of variables for radar chart.
frame : {'circle', 'polygon'}
Shape of frame surrounding axes.
"""
# calculate evenly-spaced axis angles
theta = np.linspace(0, 2*np.pi, num_vars, endpoint=False)
class RadarTransform(PolarAxes.PolarTransform):
def transform_path_non_affine(self, path):
# Paths with non-unit interpolation steps correspond to gridlines,
# in which case we force interpolation (to defeat PolarTransform's
# autoconversion to circular arcs).
if path._interpolation_steps > 1:
path = path.interpolated(num_vars)
return Path(self.transform(path.vertices), path.codes)
class RadarAxes(PolarAxes):
name = 'radar'
PolarTransform = RadarTransform
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# rotate plot such that the first axis is at the top
self.set_theta_zero_location('N')
def fill(self, *args, closed=True, **kwargs):
"""Override fill so that line is closed by default"""
return super().fill(closed=closed, *args, **kwargs)
def plot(self, *args, **kwargs):
"""Override plot so that line is closed by default"""
lines = super().plot(*args, **kwargs)
for line in lines:
self._close_line(line)
def _close_line(self, line):
x, y = line.get_data()
# FIXME: markers at x[0], y[0] get doubled-up
if x[0] != x[-1]:
x = np.append(x, x[0])
y = np.append(y, y[0])
line.set_data(x, y)
def set_varlabels(self, labels):
self.set_thetagrids(np.degrees(theta), labels)
def _gen_axes_patch(self):
# The Axes patch must be centered at (0.5, 0.5) and of radius 0.5
# in axes coordinates.
if frame == 'circle':
return Circle((0.5, 0.5), 0.5)
elif frame == 'polygon':
return RegularPolygon((0.5, 0.5), num_vars,
radius=.5, edgecolor="k")
else:
raise ValueError("Unknown value for 'frame': %s" % frame)
def _gen_axes_spines(self):
if frame == 'circle':
return super()._gen_axes_spines()
elif frame == 'polygon':
# spine_type must be 'left'/'right'/'top'/'bottom'/'circle'.
spine = Spine(axes=self,
spine_type='circle',
path=Path.unit_regular_polygon(num_vars))
# unit_regular_polygon gives a polygon of radius 1 centered at
# (0, 0) but we want a polygon of radius 0.5 centered at (0.5,
# 0.5) in axes coordinates.
spine.set_transform(Affine2D().scale(.5).translate(.5, .5)
+ self.transAxes)
return {'polar': spine}
else:
raise ValueError("Unknown value for 'frame': %s" % frame)
register_projection(RadarAxes)
return theta
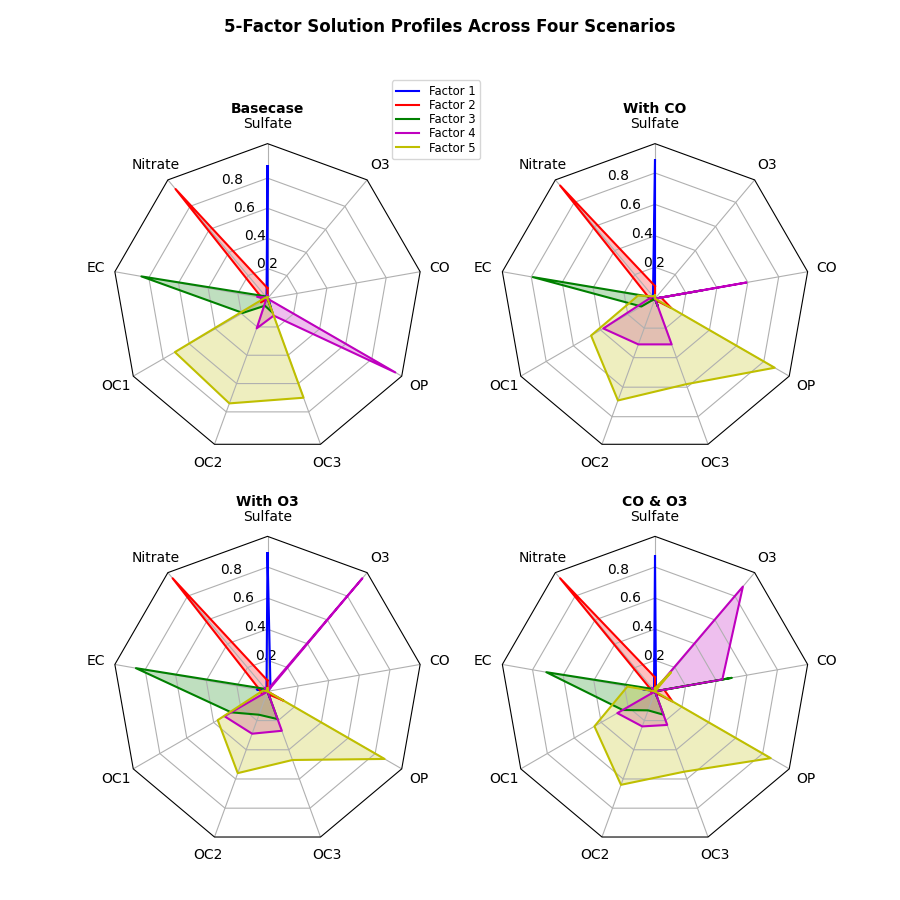
def example_data():
# The following data is from the Denver Aerosol Sources and Health study.
# See doi:10.1016/j.atmosenv.2008.12.017
#
# The data are pollution source profile estimates for five modeled
# pollution sources (e.g., cars, wood-burning, etc) that emit 7-9 chemical
# species. The radar charts are experimented with here to see if we can
# nicely visualize how the modeled source profiles change across four
# scenarios:
# 1) No gas-phase species present, just seven particulate counts on
# Sulfate
# Nitrate
# Elemental Carbon (EC)
# Organic Carbon fraction 1 (OC)
# Organic Carbon fraction 2 (OC2)
# Organic Carbon fraction 3 (OC3)
# Pyrolyzed Organic Carbon (OP)
# 2)Inclusion of gas-phase specie carbon monoxide (CO)
# 3)Inclusion of gas-phase specie ozone (O3).
# 4)Inclusion of both gas-phase species is present...
data = [
['Sulfate', 'Nitrate', 'EC', 'OC1', 'OC2', 'OC3', 'OP', 'CO', 'O3'],
('Basecase', [
[0.88, 0.01, 0.03, 0.03, 0.00, 0.06, 0.01, 0.00, 0.00],
[0.07, 0.95, 0.04, 0.05, 0.00, 0.02, 0.01, 0.00, 0.00],
[0.01, 0.02, 0.85, 0.19, 0.05, 0.10, 0.00, 0.00, 0.00],
[0.02, 0.01, 0.07, 0.01, 0.21, 0.12, 0.98, 0.00, 0.00],
[0.01, 0.01, 0.02, 0.71, 0.74, 0.70, 0.00, 0.00, 0.00]]),
('With CO', [
[0.88, 0.02, 0.02, 0.02, 0.00, 0.05, 0.00, 0.05, 0.00],
[0.08, 0.94, 0.04, 0.02, 0.00, 0.01, 0.12, 0.04, 0.00],
[0.01, 0.01, 0.79, 0.10, 0.00, 0.05, 0.00, 0.31, 0.00],
[0.00, 0.02, 0.03, 0.38, 0.31, 0.31, 0.00, 0.59, 0.00],
[0.02, 0.02, 0.11, 0.47, 0.69, 0.58, 0.88, 0.00, 0.00]]),
('With O3', [
[0.89, 0.01, 0.07, 0.00, 0.00, 0.05, 0.00, 0.00, 0.03],
[0.07, 0.95, 0.05, 0.04, 0.00, 0.02, 0.12, 0.00, 0.00],
[0.01, 0.02, 0.86, 0.27, 0.16, 0.19, 0.00, 0.00, 0.00],
[0.01, 0.03, 0.00, 0.32, 0.29, 0.27, 0.00, 0.00, 0.95],
[0.02, 0.00, 0.03, 0.37, 0.56, 0.47, 0.87, 0.00, 0.00]]),
('CO & O3', [
[0.87, 0.01, 0.08, 0.00, 0.00, 0.04, 0.00, 0.00, 0.01],
[0.09, 0.95, 0.02, 0.03, 0.00, 0.01, 0.13, 0.06, 0.00],
[0.01, 0.02, 0.71, 0.24, 0.13, 0.16, 0.00, 0.50, 0.00],
[0.01, 0.03, 0.00, 0.28, 0.24, 0.23, 0.00, 0.44, 0.88],
[0.02, 0.00, 0.18, 0.45, 0.64, 0.55, 0.86, 0.00, 0.16]])
]
return data
if __name__ == '__main__':
N = 9
theta = radar_factory(N, frame='polygon')
data = example_data()
spoke_labels = data.pop(0)
fig, axs = plt.subplots(figsize=(9, 9), nrows=2, ncols=2,
subplot_kw=dict(projection='radar'))
fig.subplots_adjust(wspace=0.25, hspace=0.20, top=0.85, bottom=0.05)
colors = ['b', 'r', 'g', 'm', 'y']
# Plot the four cases from the example data on separate axes
for ax, (title, case_data) in zip(axs.flat, data):
ax.set_rgrids([0.2, 0.4, 0.6, 0.8])
ax.set_title(title, weight='bold', size='medium', position=(0.5, 1.1),
horizontalalignment='center', verticalalignment='center')
for d, color in zip(case_data, colors):
ax.plot(theta, d, color=color)
ax.fill(theta, d, facecolor=color, alpha=0.25, label='_nolegend_')
ax.set_varlabels(spoke_labels)
# add legend relative to top-left plot
labels = ('Factor 1', 'Factor 2', 'Factor 3', 'Factor 4', 'Factor 5')
legend = axs[0, 0].legend(labels, loc=(0.9, .95),
labelspacing=0.1, fontsize='small')
fig.text(0.5, 0.965, '5-Factor Solution Profiles Across Four Scenarios',
horizontalalignment='center', color='black', weight='bold',
size='large')
plt.show()
参考
此示例中显示了以下函数、方法、类和模块的使用:
脚本总运行时间:(0分1.611秒)